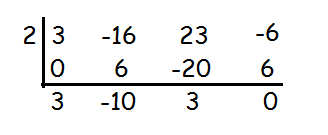
Let us solve the given cubic equation using synthetic division.
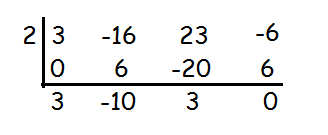
We ge the zero remainder by applying the value of x as 2. So, (x - 2) is a factor.
The factors are (x - 2) (3x 2 - 10x + 3)
By factoring the quadratic equation, we get
= 3x 2 - 1x - 9x + 3
= x (3x - 1) - 3(3x - 1)
Hence the values of x are 2, 3 and 1/3.
General form of polynomial of 4th degree.
ax 4 + bx 3 + cx 2 + dx + e = 0
α β + α γ + α δ + β γ + β δ + γ δ = c/a
α β γ + α β δ + α γ δ + β γ δ = -d/a
Find the sum of squares of roots of the equation :
2x 4 - 8x 3 + 6x 2 - 3 = 0
By comparing the given equation with general form of polynomial of degree 4, we get
a = 2, b = -8, c = 6 and d = -3
α + β + γ + δ = -b/a = 8/2 = 4
α β + α γ + α δ + β γ + β δ + γ δ = c/a = 6/2 = 3
We have to find
Ap plying the algebraic identity α 2 + β 2 + γ 2 + δ 2
(a+b+c+d) 2 = a 2 +b 2 +c 2 +d 2 + 2(ab + ac + ad + bc + bd + cd)
( α + β + γ + δ ) 2 = α 2 + β 2 + γ 2 + δ 2 + 2 ( α β + α γ + α δ + β γ + β δ + γ δ )
α 2 + β 2 + γ 2 + δ 2 = ( α + β + γ + δ ) 2 - 2 ( α β + α γ + α δ + β γ + β δ + γ δ )
α 2 + β 2 + γ 2 + δ 2 = (4) 2 - 2 (3)
Hence the sum of squares of roots of the equation is 10.
Solve the equation x 3 - 9x 2 + 14x + 24 = 0 if it is given that two of its roots are in the ratio 3: 2.
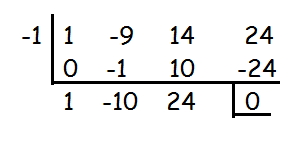
-1 is one of the roots of the cubic equation.By factoring the quadratic equation x 2 - 10x + 24, we may get the other roots.
x 2 - 10x + 24 = x 2 - 6x - 4x + 24
x - 4 = 0 and x - 6 = 0
Hence the roots of the cubic equation are -1, 4 and 6.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
© All rights reserved. onlinemath4all.com